Questão 1
2016 – FCC – Copergás-PE – Analista Contador
Em um plano de pagamento com base no Sistema de Amortização Constante − SAC observa-se que ele corresponde a um empréstimo de um determinado valor a uma taxa de 2% ao mês, a ser liquidado por meio de 60 prestações mensais e consecutivas, vencendo a primeira prestação 1 mês após a data da concessão do empréstimo. Se o valor da penúltima prestação é igual a R$ 2.600,00, então o valor da 25a prestação é, em reais, igual a a) 4.300,00. b) 3.800,00. c) 4.350,00. d) 3.850,00. e) 3.950,00.
Resolvendo a questão
Como dito no enunciado, a amortização é constante, ou seja, durante todo o período de financiamento o valor mensal a ser amortizado permanecerá o mesmo.
Vale lembrar que o valor a ser pago em cada prestação é calculado pela soma da amortização com os juros do período.
Sendo assim, temos que o valor da dívida (D) foi dividido em 60 partes iguais (D/60), a serem amortizadas mensalmente.
Ao final de cada período devemos subtrair, do saldo devedor, o amortizado no período anterior, até que na última prestação reste saldo 0 (zero).
A questão nos passa os seguintes dados:
- Valor da dívida = D
- taxa = 2% a.m. = 2/100
- período: 60 meses
- Prestação nº 59 = 2.600,00
- Prestação nº 25 = ?
Vejamos como fica nossa tabela após lançar os dados da questão:
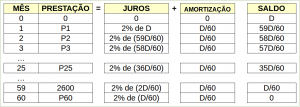
Tabela Sistema de Amortização Constante – SAC
Perceba que após o pagamento da 1ª prestação (P1), o saldo inicial (D) sofre uma redução correspondente ao valor da amortização (D/60).
Para esse cálculo, temos que:

E assim sucessivamente, até que no 59º mês reste justamente o valor da amortização (D/60), que ao ser subtraído por D/60 no fim do 60º mês extinguirá a dívida (D=0).
Para ficar mais fácil a compreensão, vamos colocar a seguinte situação problema, seguida da tabela SAC:
Uma dívida de R$ 50.000,00 foi parcelada em 5 meses com o 1º pagamento para daqui a 30 dias. Os juros praticados são de 10% ao mês e é utilizado o Sistema de Amortização Constante – SAC
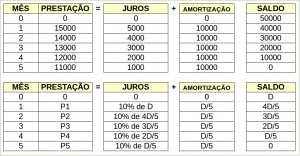
Tabela sistema de amortização constante (SAC) – como calcular
Identifique os campos similares nas duas tabelas e perceba como é feito o cálculo de cada componente envolvido.
Feito isto, voltemos à questão para resolvê-la.
Sabendo-se que o valor da prestação é calculado somando-se os juros com a amortização e, conhecido o valor da prestação nº 59, vamos calcular o valor da dívida:

Descoberto o valor da dívida (D) podemos descobrir o valor de qualquer outro componente da tabela.
Para facilitar o cálculo, vamos descobrir o valor da amortização (D/60): 150.000 / 60 = 2.500
Como a questão pede o valor da 25ª prestação (P25)

Gabarito: letra a)
Questão 2
2016 – CESPE – TCE-SC – Auditor Fiscal de Controle Externo – Contabilidade
Um financiamento de R$ 10.000 foi feito pelo sistema de amortização constante (SAC) em 5 meses consecutivos e com 2 meses de carência. A operação foi contratada à taxa de juros de 8% ao mês. Nessa situação, o valor da segunda prestação após o início da amortização era inferior a R$ 2.500. ( ) Certo ( ) Errado
Resolvendo a questão
Período de carência é o período onde não há o pagamento da AMORTIZAÇÃO DA DÍVIDA, neste período pode ou não haver o pagamento dos juros, trazendo aí 2 possibilidades quanto ao tratamento dado a eles:
- JUROS CAPITALIZADOS
- JUROS NÃO CAPITALIZADOS
Ocorre a capitalização dos juros quando este incorpora-se ao saldo devedor, mês a mês, enquanto perdurar a carência. Há um aumento no saldo em virtude do acúmulo dos juros. Não há pagamento algum por parte do tomador do empréstimo neste período.
Em sentido oposto, a NÃO capitalização dos juros se dá pelo pagamento dos juros durante o período de carência. Os juros NÃO são acrescidos ao saldo devedor. O tomador do empréstimo paga os juros correspondentes ao final de cada período e o saldo devedor permanece o mesmo.
Como a questão não especificou o tratamento dado aos juros, vamos elaborar das 2 formas
1º) com os juros capitalizados
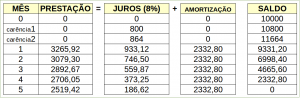
Tabela sistema de amortização constante com carência – juros capitalizados
2º) com os juros NÃO capitalizados
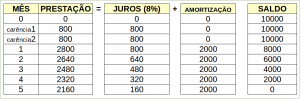
Tabela sistema de amortização constante com carência – juros NÃO capitalizados
Perceba que, em ambas, a 2ª prestação (P2) ficou superior a 2.500.
Legal, a tabela ajuda bastante a entender mas…
e na hora da prova, tem que construir toda a tabela??????
Claro de não!
Basta você seguir o seguinte raciocínio, sem fórmulas mirabolantes, como já explicado na tabela da questão 1.
- Comece pela coluna do saldo da dívida (D). O valor da última linha é 0 (zero), o que caracteriza a liquidação da dívida;
- Preencha a linha imediatamente acima com o valor da dívida dividido pelo número de prestações (D/n), que, ao subtrair com o valor da amortização (D/n) dará resultado 0 (zero), como já colocado na última linha;
- À medida que for subindo de linha, vá acrescentando uma unidade multiplicadora à variável “D/n” (2D/n, 3D/n, 4D/n, etc.) até chegar a nD/n (ou seja, D);
- Lembre-se que os juros são calculados com base no saldo final do período imediatamente anterior (se você está na linha em que o saldo final é “2D/n”, os juros deste período serão calculados sobre o saldo “3D/n”, que está na linha imediatamente acima);
- A partir daí, entendendo a sequência lógica da coluna do saldo devedor e do cálculo dos juros, basta fazer a correlação com a linha que indica a prestação a ser encontrada; e
- Não esquecer que o valor da prestação é calculado pela soma dos juros com a amortização (D/n).
Gabarito: ERRADA
Questão 3
Uma agência bancária, ao emprestar a quantia de R$ 60.000,00 a uma empresa, entregou o valor no ato e concedeu à empresa 3 anos de carência, sem que os juros desse período ficassem capitalizados para serem pagos posteriormente. Com base nessa situação e sabendo que esse empréstimo será pago pelo sistema de amortização constante (SAC), em 3 anos e à taxa de juros de 10% ao ano, julgue os itens subsecutivos. O total de juros pagos será superior a R$ 23.000,00. ( ) Certo ( ) Errado
Resolvendo a questão
Aqui o examinador deixa claro que os juros no período da carência NÃO serão capitalizados, ou seja, serão pagos ao fim de cada um dos 3 anos da carência, de modo que não será acrescido ao saldo devedor.
Com base nos dados da questão e em tudo que já foi visto sobre a construção da tabela SAC com carência e com juros não capitalizados, resta-nos, de imediato, liquidar de vez a questão.
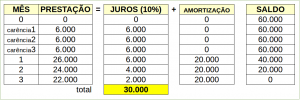
Tabela sistema de amortização constante com carência e juros NÃO capitalizados
Somando-se os juros pagos durante todo o período, acha-se o valor de R$ 30.000, que é superior a R$ 23.000.
Gabarito: CERTO
Bons estudos! 😉
Se você gostou do post, deixe seu comentário abaixo, curta e compartilhe com seus amigos.
Vocẽ quer multiplicar sua capacidade de aprendizagem ???Clique aqui e baixe agora nosso modelo de Ficha de Arquivo para fazer seu fichamento.
Ótima explicação!!!!
Muito obrigado pelo comentário Amanda,
agradeço sua visita e volte sempre.
Grande abraço
e bons estudos